応力三軸度とは、材料内部の応力の状態を示す値です。その値によって、材料の変形や破壊に大きな影響があります。
引っ張り試験での破断伸びが10%の材料でも、常に10%伸びると破断するわけではなく、1%で壊れたり、50%伸ばしても壊れないこともあります。
この理由は、応力三軸度を知ると理解できます。
機械や構造物を設計する際は、少なくともその概念だけでも知っておくと良いと思います。
5歳児は応力三軸度を知っている?
3歳児に粘土を持たせて、長く伸ばしてごらんと言ってみます。
すると両端を持って引っ張り、ブチっと切れてしまいました。

次に、5歳児に同じように言ってみます。
すると、粘土をモミモミしながら、見事に長く伸ばすことに成功しました。

5歳児は、これまでの粘土遊びの経験から、粘土は引っ張ると切れてしまうことを学習済みでした。
同じだけ伸ばしても(=長さ方向のひずみが同じでも)、引っ張って伸ばすと切れ、側面を押すことで伸ばす場合は切れない。
その理由は、材料が周囲から圧縮力を受けた状態の方が、切れるまでの伸びを大きく取れるためです。
材料が圧縮されているのか、膨張する方向に力が働いているのか、その程度は、応力三軸度という一つの値で判ります。
3歳児の方法は、1軸引っ張りであり、応力三軸度は、0.33となります。
5歳児の方法は、2軸圧縮であり、応力三軸度は、-0.66となります。
ちなみに、粘土板に押し付けて転がしながら伸ばす方法もありますが、この場合は、1軸圧縮であり、応力三軸度は-0.33となります。
基本的に応力三軸度が低いほど、破断伸びが大きくなります。
(但し、応力三軸度がおおよそ-0.33~0.33の範囲では、せん断破壊が支配的になるため破断伸びが低下することもあります)
ということで、だいたい5歳位で誰でも、応力三軸度ことは知らなくても、その概念は体得済みなわけです。
応力三軸度の定義
応力三軸度 \(\displaystyle η\) は下記の式で表されます。
\(\displaystyle η=\frac{ σ_k }{ σ_{eq} }\)
ここで、\(\displaystyle σ_k\)は、平均応力(静水圧力)で、
\(\displaystyle σ_k=\frac{ 1 }{3}( σ_1+σ_2+σ_3)\)
であり、\(\displaystyle σ_1~σ_3\) は、主応力です。
\(\displaystyle σ_{eq}\)はMises相当応力で、
\(\displaystyle σ_{eq}=\sqrt{\frac{ 1 }{ 2}\{(σ_1-σ_2)^2+(σ_2-σ_3)^2+(σ_3-σ_1)^2\}}\)
とあらわされます。
応力三軸度は上式から、平均応力と相当応力の比
と言われますが、これだとどうもピンときません。
引張応力が多方向に生じている場合、上辺は大きくなり、下辺は、主応力の差なので小さくなります。
この除算により、応力の大きさを排除し、応力の多軸性のみを表現した値にしている。
と考えると理解しやすいのではないでしょうか。
また、正規化(無次元化)した値なので、単位系などによらず応力の多軸性の影響を考えやすくなります。
典型的な荷重状態と応力三軸度
応力の状態によって、破壊ひずみは変化します。破壊するときの応力三軸度により、破面にも違いが現れます。
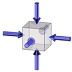
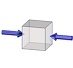
| 3軸等圧縮 (静水圧) |
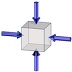
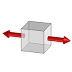
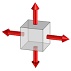
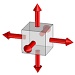
2軸等圧縮 | 1軸圧縮 | 単純せん断 | 1軸引張 | 2軸等引張 | 3軸等引張 | |
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
||
| 応力三軸度 | -∞ | -0.666… | -0.333… | 0 | 0.333… | 0.666… | ∞ |
| 破壊ひずみ | 破壊しない | 例) 100% |
例) 20% |
例) 15% |
例) 5% |
例) 1%未満 |
|
| 典型的な破面 | <すべり面分離> | <等軸ディンプル> | |||||
| <シアーディンプル> | <脆性(へき開)> | ||||||
注:破壊ひずみの数値はイメージを掴みやすくするために記載したもので、実際のデーターではありません。
応力三軸度をどうやって調べるか
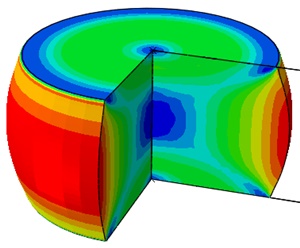
応力三軸度を現物で計測するのは困難なため、FEM(有限要素法)で解析します。
下記は、切り欠きのある薄板に、上下方向に引張荷重を加えたときの、Mises応力と応力三軸度です。
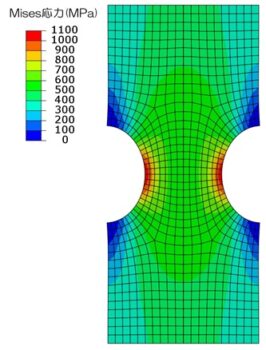
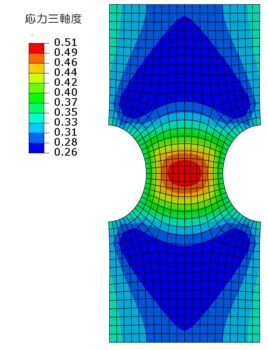
応力集中部は応力三軸度が高くなる
応力集中部付近は応力三軸度が大きくなります。
応力集中部には力の流れが集まってくるので、下図の矢印の向きの力が働くからです。
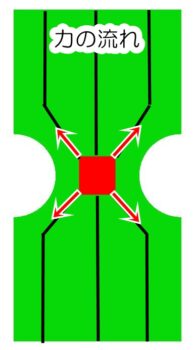 切り欠き部は伸ばされると同時に細くなろうとしますが、周辺の部分が細くなるのを阻止しようとするので、左右方向の引張応力が高くなるというように考えることもできます。
切り欠き部は伸ばされると同時に細くなろうとしますが、周辺の部分が細くなるのを阻止しようとするので、左右方向の引張応力が高くなるというように考えることもできます。
応力三軸度の活用
構造設計
上記の解析例のとおり、応力集中部には力の流れが集中するので、荷重の方向以外の方向の応力が大きくなり、応力三軸度が大きくなります。
多軸の応力によって塑性拘束が起こり、降伏点が上がって塑性変形が起こりにくくなる一方、小さな変形で破壊を起こしやすくなります。
変形を伴わず予兆なく破壊する可能性が高い部位は、FMEAの影響度を高くするべきです。
応力三軸度を調べることで、危険度の高い部位を設計段階で知ることができます。
塑性加工での破壊予測
塑性加工では材料の破壊ひずみ以上のひずみが生じる変形を加えると、加工中の損傷が起こると考えられます。しかし、前途の通り、破壊ひずみは応力三軸度によって変わることから、加工限界をより精度良く予測するために応力三軸度を考慮することが有効です。
加工の進展とともに応力三軸度が変化するので、ある時間でのひずみと応力三軸度からダメージを計算し、それを全工程分積分することで、破壊に至るかを推定することができます。
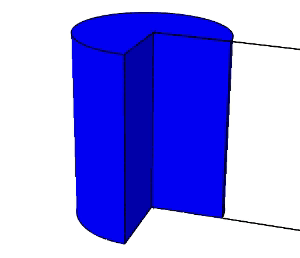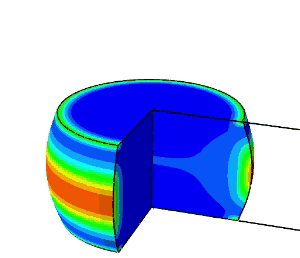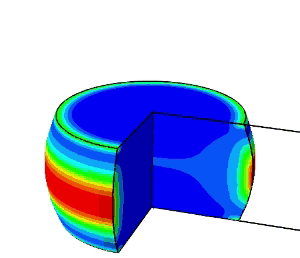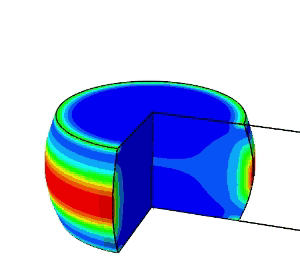
上図は、据え込み加工の検討例で、ダメージの大きい部分が赤色で表示されています。
破壊しないようにするには応力三軸度が下がるようにすれば良いわけです。
鍛造加工なら、自由鍛造より型鍛造の方が応力三軸度が低くなります。プレス加工で応力三軸度を下げるには、材料を油圧で押さえるファインブランキング加工などもあります。
応力三軸度の限界
応力三軸度についての研究では、応力三軸度と破壊ひずみ(延性限界)の関係を定式化しようとの試みが多くあります。
しかし、応力三軸度が0~0.33の範囲では、応力三軸度が大きくなると破壊ひずみが小さくなる結果のものと、その逆の変化になるというものがあり、まだ確固たるものは有りません。
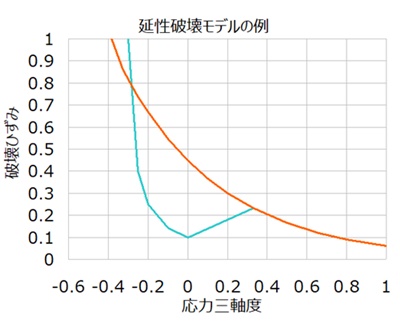
応力三軸度が-0.33~0.33の範囲はせん断が支配的な応力状態なので、垂直方向の平均応力の状態を示す応力三軸度だけでは、延性限界や破壊を示せないためだと思います。
破壊という非常に複雑な現象をたった一つの数値で表すのは、少々無理があり、材料固有の特性をラボで求めるのもかなり困難なようです。
実際の機械部品設計で応力三軸度を使った検討をする場合、FEM解析での損傷予測計算と実験を繰り返して、理論式で同定するなどにより材料特性を修正していく必要があります。
まとめ