断面二次モーメントと断面係数の公式が最速で判るページです。
下記の図をクリックすると公式と計算式に飛びます。便利な計算フォームも設置しました。
正多角形ははこちらです。
断面二次モーメント、断面係数の公式と計算フォーム
正方形
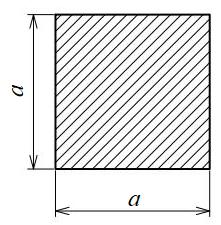
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ 1 }{ 12 }a^{ 4 }\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \frac{ a }{ \sqrt{12} } =0.2886751a\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{ 1 }{ 6 }a^{ 3 }\) |
| 面積\(\displaystyle A\) | \(\displaystyle a^{ 2 }\) |
計算フォーム
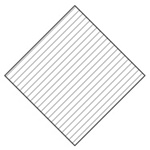
正方形45°
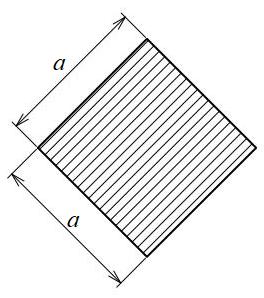
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ 1 }{ 12 }a^{ 4 }\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \frac{ a }{ \sqrt{12} } =0.2886751a\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{ 1 }{ 6\sqrt{2} }a^{ 3 }\) |
| 面積\(\displaystyle A\) | \(\displaystyle a^{ 2 }\) |
計算フォーム
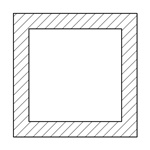
正方形中空
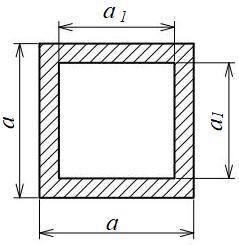
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ 1 }{ 12 }(a^{4 }-a_{1}^{4})\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{ 1 }{ 12 }(a^{ 2 }+a_{1}^{2})}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{ 1 }{ 6a }(a^{4 }-a_{1}^{4})\) |
| 面積\(\displaystyle A\) | \(\displaystyle a^{ 2 }-{a_{1}}^{2}\) |
計算フォーム
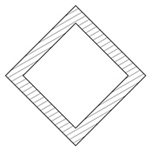
正方形中空45°
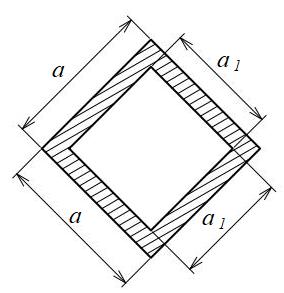
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ 1 }{ 12 }(a^{4 }-a_{1}^{4})\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{ 1 }{ 12 }(a^{ 2 }+a_{1}^{2})}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{ \sqrt{2} }{ 12a }(a^{4 }-a_{1}^{4})\) |
| 面積\(\displaystyle A\) | \(\displaystyle a^{ 2 }-{a_{1}}^{2}\) |
計算フォーム
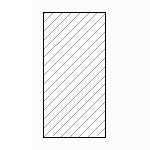
四角形、長方形断面
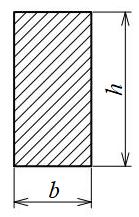
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ 1 }{ 12 }bh^{ 3 }\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \frac{ h }{ \sqrt{12} } =0.2886751h\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{ 1 }{ 6 }bh^{ 2 }\) |
| 面積\(\displaystyle A\) | \(\displaystyle bh\) |
計算フォーム
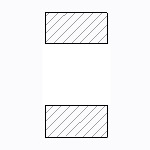
四角形(中空き)断面
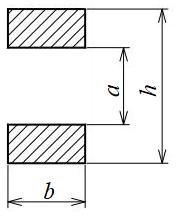
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ b }{ 12 }(h^{ 3 }-a^{3})\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{h^{ 3 }-a^{3}}{12(h-a)}}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{b(h^{ 3 }-a^{3})}{6h}\) |
| 面積\(\displaystyle A\) | \(\displaystyle b(h-a)\) |
計算フォーム
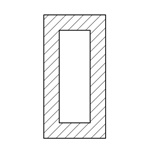
長方形断面(中空)
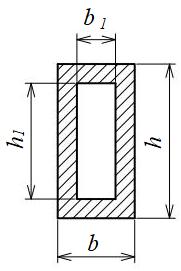
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ 1 }{ 12 }(bh^{ 3 }-{b_1}{h_1}^{3})\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{ bh^{ 3 }-{b_1}{h_1}^{3} }{ 12(bh-{b_1}{h_1}) }}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{ bh^{ 3 }-{b_1}{h_1}^{3} }{ 6h }\) |
| 面積\(\displaystyle A\) | \(\displaystyle bh-b_{1}h_{1}\) |
計算フォーム
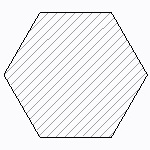
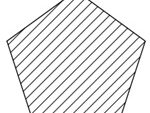
六角形断面(1)
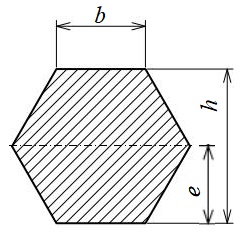
\(\displaystyle h=\sqrt{3}b\)
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{5\sqrt{3}}{16}b^{4}=0.5412658b^{4}\) |
|---|---|
| \(\displaystyle \frac{5\sqrt{3}}{144}h^{4}=0.06014065h^{4}\) | |
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{ 5 }{ 24 }}b =0.4564355b\) |
| \(\displaystyle \sqrt{\frac{ 5 }{ 72 }}h =0.2635231h\) | |
| 断面係数\(\displaystyle Z\) | \(\displaystyle e=\frac{\sqrt{3}}{2}b =0.8660254b\)
\(\displaystyle Z=\frac{5}{8}b^{3}\)\(\displaystyle =0.625b^{3}\) |
| \(\displaystyle e=\frac{1}{2}h =0.5h\)
\(\displaystyle Z=\frac{5\sqrt{3}}{72}h^{3} =0.1202813h^{3}\) |
|
| 面積\(\displaystyle A\) | \(\displaystyle \frac{3\sqrt{3}}{2}b^{ 2 }\) |
| \(\displaystyle \frac{\sqrt{3}}{2}h^{ 2 }\) |
計算フォーム
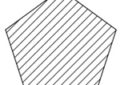
六角形断面(2)
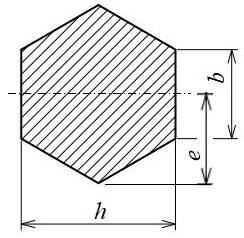
\(\displaystyle h=\sqrt{3}b\)
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{5\sqrt{3}}{16}b^{4} =0.5412658b^{4}\) |
|---|---|
| \(\displaystyle \frac{5\sqrt{3}}{144}h^{4} =0.06014065h^{4}\) | |
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{ 5 }{ 24 }}b =0.4564355b\) |
| \(\displaystyle \sqrt{\frac{ 5 }{ 72 }}h =0.2635231h\) | |
| 断面係数\(\displaystyle Z\) | \(\displaystyle e=b\)
\(\displaystyle |
| \(\displaystyle e=\frac{h}{\sqrt{3}}\)
\(\displaystyle |
|
| 面積\(\displaystyle A\) | \(\displaystyle \frac{3\sqrt{3}}{2}b^{ 2 }\) |
| \(\displaystyle \frac{\sqrt{3}}{2}h^{ 2 }\) |
計算フォーム
円形断面
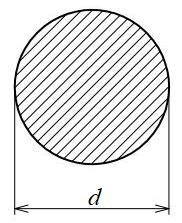
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ \pi }{ 64 }d^{ 4 }\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{ 1 }{ 16 }}d\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{ \pi }{ 32 }d^{ 3 }\) |
| 面積\(\displaystyle A\) | \(\displaystyle \frac{\pi}{4}d^{ 2 }\) |
計算フォーム
円形(中空)断面
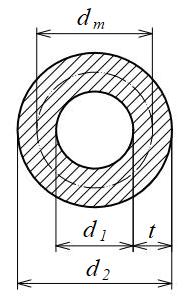
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ \pi }{ 64 }({d_2}^{ 4 }-{d_1}^{4})\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{ 1 }{ 16 }({d_2}^{ 2 }+{d_1}^{2})}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{ \pi }{ 32 }\frac{({d_2}^{ 4 }-{d_1}^{4})}{{d_2}}\)
\(≒ {0.8d_m}^{2}t\) \(\displaystyle (t/d_m\)が小さいとき) |
| 面積\(\displaystyle A\) | \(\displaystyle \frac{\pi}{4}(d^{ 2 }-d_{1}^{2})\) |
計算フォーム
八角形断面
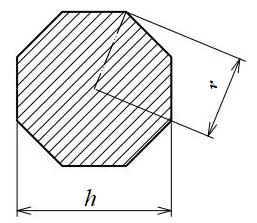
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{1+2\sqrt{2}}{6}r^4 =0.6380712r^{4}\)
\(\displaystyle \frac{4\sqrt{2}-5}{12}h^4 =0.05473785h^{4}\) |
|---|---|
| 断面二次半径\(\displaystyle k\)
\(\displaystyle k=\sqrt{\frac{I}{A}}\) |
\(\displaystyle 0.4749655r\)
\(\displaystyle 0.2570495h\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle 0.6906433r^{3}\)
\(\displaystyle 0.1094757h^{3}\) |
| 面積\(\displaystyle A\) | \(\displaystyle 2\sqrt{2}r^{2}\)
\(\displaystyle 2(\sqrt{2}-1)h^{2}\) |
計算フォーム
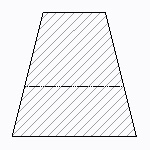
台形断面
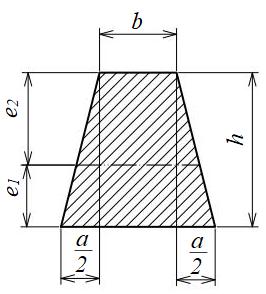
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{a^{2}+6ab+6b^{2}}{36(a+2b)}h^{3}\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \frac{h}{a+2b}\sqrt{\frac{a^{2}+6ab+6b^{2}}{18}}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle e_{1}=h-e_{2} =\frac{1}{3}\frac{a+3b}{a+2b}h\)
\(\displaystyle e_{2}=\frac{1}{3}\frac{2a+3b}{a+2b}h\) \(\displaystyle Z_{1}=I/e_{1} =\frac{a^{2}+6ab+6b^{2}}{12(a+3b)}h^{2}\) \(\displaystyle Z_{2}=I/e_{2} =\frac{a^{2}+6ab+6b^{2}}{12(2a+3b)}h^{2}\) |
| 面積\(\displaystyle A\) | \(\displaystyle (\frac{a}{2}+b)h\) |
長さの短い辺(上図では上辺)側の応力は、Z2を使い、長さの短い側(上図では下辺)側の応力はZ1を使って計算します。
計算フォーム
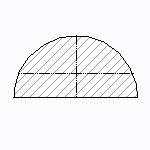
半円形断面
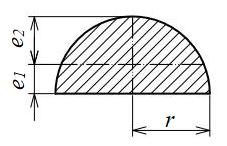
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle (\frac{\pi}{8}-\frac{8}{9\pi})r^4 =0.1097570r^4\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle r\sqrt{\frac{9\pi^2-64}{36\pi^2}} =0.264336r\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle e_1=\frac{4r}{3\pi} =0.4244132r\)
\(\displaystyle e_2=\frac{3\pi-4}{3\pi}=0.5755868r\) \(\displaystyle Z_1=0.2586087r^3\) \(\displaystyle Z_2=0.1906871r^3\) |
| 面積\(\displaystyle A\) | \(\displaystyle \frac{\pi}{2}r^{ 2 }\) |
計算フォーム
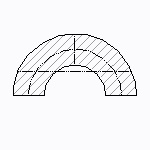
円弧型断面
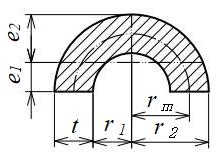
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle 0.1098({r_2}^4-{r_1}^4)\)
\(\displaystyle -\frac{0.283{r_2}^2{r_1}^2(r_2-r_1)}{r_2+r_1}\) \(\displaystyle ≒0.3t・{r_m}^3\) \(\displaystyle (t/r_mが小さい時)\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{I}{A}}\)
\(\displaystyle ≒0.31r_m\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle e_1=\frac{4({r_2}^2+r_2r_1+{r_1}^2)}{3\pi(r_2+r_1)}\)
\(\displaystyle e_2=r_2-e_1\) \(\displaystyle Z_1=I/e_1\) \(\displaystyle Z_2=I/e_2\) |
| 面積\(\displaystyle A\) | \(\displaystyle \frac{\pi}{2}(r_{2}^{ 2 }-r_{1}^{2})\) |
計算フォーム
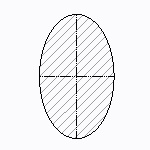
楕円形断面
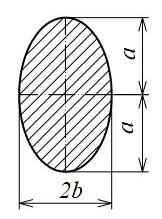
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{\pi}{4}a^3b\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \frac{a}{2}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{\pi}{4}a^2b\) |
| 面積\(\displaystyle A\) | \(\displaystyle {\pi}ab\) |
計算フォーム
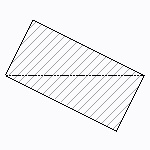
四角形断面(傾斜)
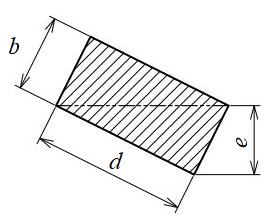
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{b^3d^3}{6(b^2+d^2)}\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle bd\sqrt{\frac{1}{6(b^2+d^2)}}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{b^2d^2}{6\sqrt{b^2+d^2}}\) |
| 面積\(\displaystyle A\) | \(\displaystyle bd\) |
計算フォーム
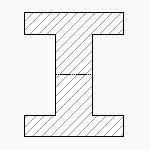
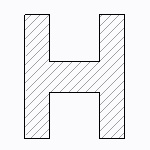
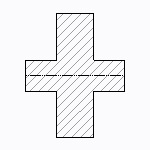
H形、十字形断面
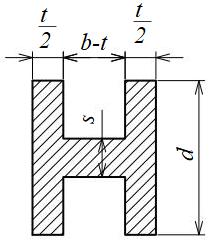
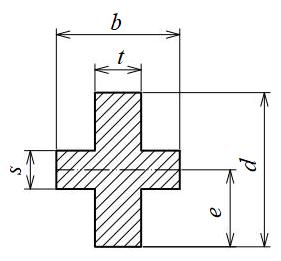
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{td^3+s^3(b-t)}{12}\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{td^3+s^3(b-t)}{12(td+s(b-t))}}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{td^3+s^3(b-t)}{6d}\) |
| 面積\(\displaystyle A\) | \(\displaystyle s(b-t)+td\) |
計算フォーム
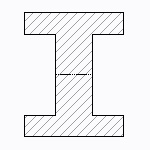
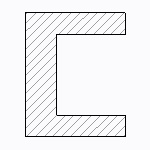
I形、チャンネル断面
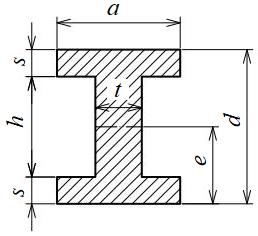
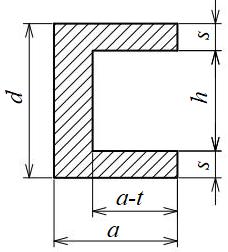
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ad^3-h^3(a-t)}{12}\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{ad^3-h^3(a-t)}{12(ad-h(a-t))}}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{ad^3-h^3(a-t)}{6d}\) |
| 面積\(\displaystyle A\) | \(\displaystyle 2sa+ht\) |
計算フォーム
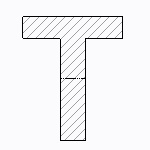
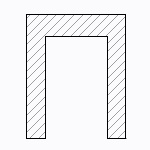
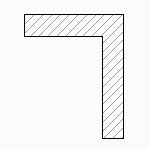
T形、チャンネル形、L形断面
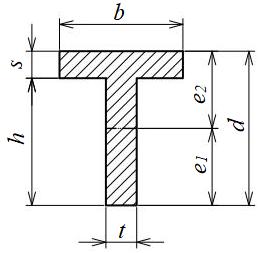
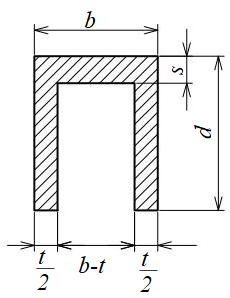
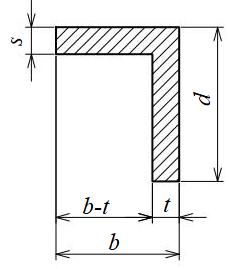
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle I=\frac{1}{3}(t{e_1}^3+b{e_2}^3\)
\(\displaystyle -(b-t)(e_2-s)^3)\) ただし、 \(\displaystyle e_1=d-\frac{d^2t+s^2(b-t)}{2(bs+ht)}\) \(\displaystyle e_2=\frac{d^2t+s^2(b-t)}{2(bs+ht)}\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{I}{A}}\)
ただし、 \(\displaystyle A=bs+ht\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle Z_1=\frac{I}{e_1}\)
\(\displaystyle Z_2=\frac{I}{e_2}\) |
| 面積\(\displaystyle A\) | \(\displaystyle bs+ht\) |
計算フォーム
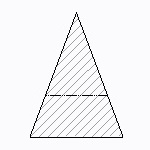
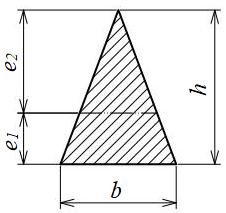
三角形断面
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{ 1 }{ 36 }bh^{ 3 }\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{ 1 }{ 18 }}h\)
\(\displaystyle (k=0.236h)\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle e_{1}=\frac{1}{3}h\)
\(\displaystyle e_{2}=\frac{2}{3}h\) \(\displaystyle \(\displaystyle Z_{2}=\frac{1}{24}bh^{2}\) |
| 面積\(\displaystyle A\) | \(\displaystyle \frac{bh}{2}\) |
e1、e2は中立軸の位置を示します。三角形の頂点側の応力は、Z2を使い、底辺側の応力はZ1を使って計算します。
計算フォーム
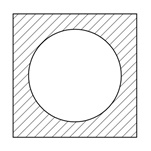
正方形(丸穴)断面
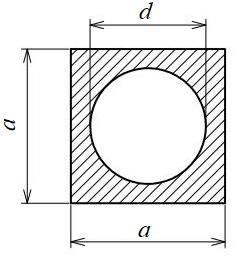
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{1}{12}(a^4-\frac{3{\pi}d^{4}}{16})\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{I}{A}}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle \frac{1}{6}(a^3-\frac{3{\pi}d^{4}}{16a})\) |
| 面積\(\displaystyle A\) | \(\displaystyle a^{2}-\frac{{\pi}d^{2}}{4}\) |