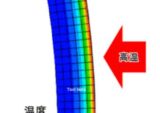
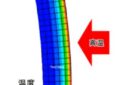
熱膨張による長さや体積の変化、熱応力についての計算式をまとめ、計算フォームを設定しました。
熱膨張の原理と身近な例、設計上の注意事項については、こちら、
熱膨張係数(線膨張係数)の一覧についてはこちら、をご覧ください。
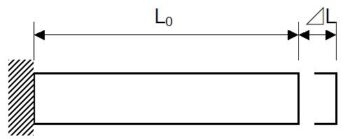
拘束なしでの熱膨張
長さや体積の変化は以下のとおりです。拘束なしの状態では熱応力は発生しません。
長さ変化
\(\displaystyle 温度差:⊿T[℃] \)
\(\displaystyle 線膨張係数:α \)[1×10-6/℃]
\(\displaystyle 元の長さ:L_0[mm] \)
\(\displaystyle 伸び:⊿L[mm] \)
\(\displaystyle ⊿L=α⊿TL_0 \)
注:温度が下がる場合は、温度差をマイナスで入れてください。伸びがマイナスの場合は収縮、プラスの場合は膨張を示します。温度は、K(ケルビン)でも換算不要です。
体積変化
\(\displaystyle 温度差:⊿T[℃] \)
\(\displaystyle 体積膨張係数:β \)[1×10-6/℃]
\(\displaystyle 元の体積:V_0 \)[mm3]
\(\displaystyle 体積の変化量:⊿V \)[mm3]
\(\displaystyle ⊿V=β⊿TV_0 \)
注:温度が下がる場合は、温度差をマイナスで入れてください。長さの変化量ががマイナスの場合は収縮、プラスの場合は膨張を示します。温度は、K(ケルビン)でも換算不要です。
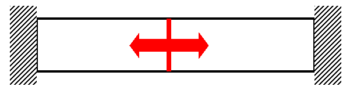
両端を拘束した棒の熱応力
\(\displaystyle 温度差:⊿T[℃] \)
\(\displaystyle 線膨張係数:α \)[1×10-6/℃]
\(\displaystyle ヤング率:E \)[MPa]
\(\displaystyle 熱応力:σ \)[MPa]
\(\displaystyle σ=α・⊿T・E \)
注:温度が下がる場合は、温度差をマイナスで入れてください。熱応力がマイナスの場合は圧縮応力、プラスの場合は引張応力を示します。温度は、K(ケルビン)でも換算不要です。
並列組み合わせ棒の熱膨張と熱応力

注:2本の部材1は対称に配置され、同形状、同材質で、断面積は2本の合計とします。部材1がパイプ状で、内部に部材2が配置されている構成でも同様に計算できます。
\(\displaystyle 温度差:⊿T[℃] \)
\(\displaystyle 部材1の線膨張係数:α_1 \)[1×10-6/℃]
\(\displaystyle 部材2の線膨張係数:α_2 \)[1×10-6/℃]
\(\displaystyle 部材1のヤング率:E_1 \)[MPa]
\(\displaystyle 部材2のヤング率:E_2 \)[MPa]
\(\displaystyle 部材1の断面積:A_1 \)[mm2]
\(\displaystyle 部材2の断面積:A_2 \)[mm2]
\(\displaystyle 元の長さ:L_0[mm] \)
\(\displaystyle 部材1の熱応力:σ_1 \)[MPa]
\(\displaystyle σ_1=-\frac{(α_1-α_2)⊿TE_1E_2A_2}{E_1A_1+E_2A_2} \)
\(\displaystyle 部材2の熱応力:σ_2 \)[MPa]
\(\displaystyle σ_1=\frac{(α_1-α_2)⊿TE_1E_2A_1}{E_1A_1+E_2A_2} \)
\(\displaystyle 伸び:⊿L[mm] \)
\(\displaystyle ⊿L=\frac{E_1A_1α_1+E_2A_2α_2}{E_1A_1+E_2A_2}⊿TL_0 \)
注:温度が下がる場合は、温度差をマイナスで入れてください。熱応力がマイナスの場合は圧縮応力、プラスの場合は引張応力を示します。温度は、K(ケルビン)でも換算不要です。
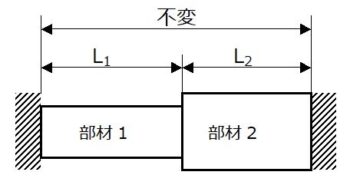
直列組み合わせ棒の熱応力
\(\displaystyle 温度差:⊿T[℃]\)
\(\displaystyle 部材1の線膨張係数:α_1 \)[1×10-6/℃]
\(\displaystyle 部材2の線膨張係数:α_2 \)[1×10-6/℃]
\(\displaystyle 部材1のヤング率:E_1 \)[MPa]
\(\displaystyle 部材2のヤング率:E_2 \)[MPa]
\(\displaystyle 部材1の断面積:A_1 \)[mm2]
\(\displaystyle 部材2の断面積:A_2\)[mm2]
\(\displaystyle 部材1の長さ:L_1[mm]\)
\(\displaystyle 部材2の長さ:L_2[mm]\)
\(\displaystyle 部材1の熱ひずみ:ε_1 \)
\(\displaystyle ε_1=-\frac{E_2A_2(α_1L_1+α_2L_2)⊿T}{E_1A_1L_2+E_2A_2L_1} \)
\(\displaystyle 部材2の熱ひずみ:ε_2 \)
\(\displaystyle ε_2=-\frac{E_1A_1(α_1L_1+α_2L_2)⊿T}{E_1A_1L_2+E_2A_2L_1} \)
\(\displaystyle 部材1の熱応力:σ_1 \)[MPa]
\(\displaystyle σ_1=ε_1E_1 \)
\(\displaystyle 部材2の熱応力:σ_2 \)[MPa]
\(\displaystyle σ_2=ε_2E_2 \)
\(\displaystyle 部材1の伸び:λ_1[mm] \)
\(\displaystyle λ_1=(α_1⊿T+ε_1)L_1 \)
\(\displaystyle 部材2の伸び:λ_2[mm] \)
\(\displaystyle λ_2=(α_2⊿T+ε_2)L_2 \)
\(\displaystyle 壁からの反力:R \)
\(\displaystyle R=σ_1A_1=σ_2A_2 \)
注:温度が下がる場合は、温度差をマイナスで入れてください。熱応力がマイナスの場合は圧縮応力、プラスの場合は引張応力を示します。温度は、K(ケルビン)でも換算不要です。