正多角形の断面積や、内接円半径、外接円半径、断面二次モーメント、断面係数などの公式をまとめました。計算フォームも設置しましたのでご活用ください。
正多角形の計算式
正多角形 (正五角形、正七角形などの計算ができます)
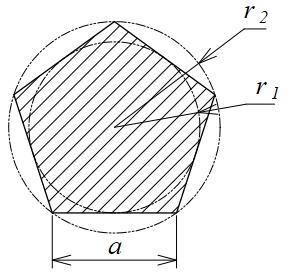
A:面積
n:辺の数
a:辺の長さ
r2:外接円の半径
r1:内接円の半径\(\displaystyle r_2=\frac{a}{2sin\frac{\pi}{n}} \)
n:辺の数
a:辺の長さ
r2:外接円の半径
r1:内接円の半径\(\displaystyle r_2=\frac{a}{2sin\frac{\pi}{n}} \)
\(\displaystyle r_1=\frac{a}{2tan\frac{\pi}{n}} \)
| 断面二次モーメント\(\displaystyle I\) | \(\displaystyle \frac{A}{24}({6r_2}^2-a^{2})\)
\(\displaystyle =\frac{A}{48}({12r_1}^2+a^{2})\) |
|---|---|
| 断面二次半径\(\displaystyle k\) | \(\displaystyle \sqrt{\frac{1}{24}({6r_2}^2-a^{2})}\) |
| 断面係数\(\displaystyle Z\) | \(\displaystyle Z_{1}=\frac{I}{r_{2}cos(\pi/n)}\)
\(\displaystyle Z_{2}=\frac{I}{r_{2}}\) \(\displaystyle ≒\frac{Ar_{2}}{4}\) |
| 面積\(\displaystyle A\) | \(\displaystyle A=\frac{na^{2}}{4tan\frac{\pi}{n}} \) |
はりの曲げにて、nが奇数の場合、頂点側の応力は、Z2を使い、辺側の応力はZ1を使って計算します。
nが偶数の場合、頂点を真下にして曲げる場合(◇)の上下の角の応力はZ2を使い、辺を真下にして曲げる場合(□)の上下の辺の応力はZ1を使って計算します。