ポアソン比は、手計算ではあまり使いませんが、FEM(有限要素法)で構造解析するときには必ず必要な数値です。
物の変形を考える上でも重要な考え方ですので、感覚的に理解しやすいようにまとめました。
ポアソン比とは?直感的な意味
ポアソン比は、荷重方向の歪と直角方向の歪の比を示す数値です。
ポアソン比を感覚的に理解するには、ゴムとコルクを潰したときの様子をイメージすると良いです。
ゴムを潰すと、横に広がります。
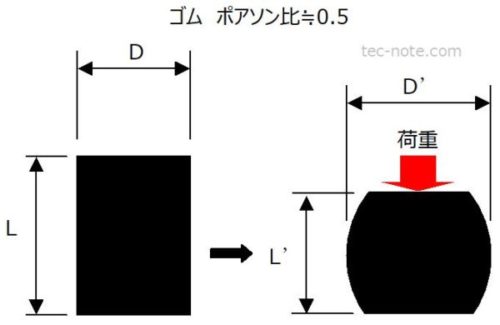
一方コルクを潰すと、横にはほとんど広がらず、体積が縮みます。
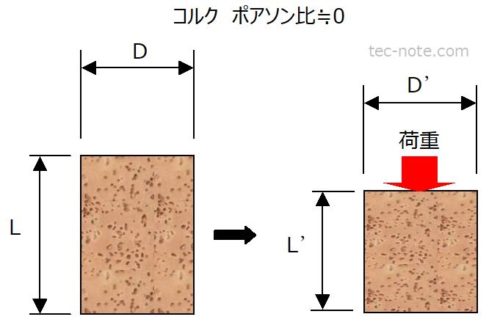
つまり、ポアソン比は荷重を加えた方向と直角方向の変形の程度を示す値です。
計算式は下記のとおりで、変形前後の歪から計算できます。
荷重方向の歪
$$\epsilon_{ L } = \frac{ L -L’}{ L } $$
直角方向の歪
$$\epsilon_{ D } = \frac{ D -D’}{ D } $$
ポアソン比(荷重方向の歪と直角方向の歪の比)
$$\nu = -\frac{ \epsilon_{ D } }{ \epsilon_{ L } } $$
$$\epsilon_{ L } = \frac{ L -L’}{ L } $$
直角方向の歪
$$\epsilon_{ D } = \frac{ D -D’}{ D } $$
ポアソン比(荷重方向の歪と直角方向の歪の比)
$$\nu = -\frac{ \epsilon_{ D } }{ \epsilon_{ L } } $$
ポアソン比νの値は、0≦ν≦0.5の範囲となります。
無次元の歪の比率ですから、ポアソン比も無次元で、単位は有りません。
ポアソン比は体積変化しやすさを示す数値でもある
ゴムとコルクの図をもう一度見てください。
ゴムの方は、体積がほとんど変わっていないのに、コルクの方は体積が減少していることに気づくと思います。
体積弾性係数 K と、縦弾性係数(ヤング率) E の間には、下記の関係があります。
$$K = \frac{ E}{ 3(1-2\nu) } $$
この式で、ポアソン比 ν が0.5に近づくと、Kは無限大になり、体積が変化し難くなることが判ります。
ポアソン比が大きい物質は、体積圧縮されずに、横に逃げる。
ポアソン比が小さい物質は、体積圧縮され、横には膨らみ難い。
ってイメージを持っておきましょう。
引張の場合も含めるとこうなります。
ポアソン比が大きい物質は、体積変化し難く、横方向に変化しやすい。
ポアソン比が小さい物質は、体積変化しやすく、横方向に変化し難い。
ポアソン比の記号
ポアソン比の記号は、上記でも使ったとおり、ギリシャ文字の
$$\nu$$
を使います。
読み方は、「ニュー」です。
ポアソン比の求め方
引張、圧縮によって、外径の変化量は下記の式で求めることができます。
$$D’ = \frac{\nu・D・(L -L’)}{ L } $$
ポアソン比は弾性範囲で用いるもので、大きな歪では使用できません。
ポアソン比0.5でも体積変化しない訳ではありませんのでご注意ください。
金属のポアソン比
金属のポアソン比はだいたい0.3程度だと思っていれば大丈夫です。
| 材質 | ポアソン比 |
|---|---|
| 炭素鋼、低合金鋼 | 0.270~0.285 |
| ステンレス鋼 SUS304 | 0.291~0.298 |
| アルミ合金 | 0.33 |